C Assignment

Here is the link for download.

Permutation in Lexicographical Order

This C program prints the permutation of n distinct objects (0 < n <= 26 )  in Lexicographical Order.

#include<stdio.h>
#include<malloc.h>
void sort(char *permutation,int n,int pos);
void replace_min (char *permutation,int n,int pos);
int main()
{
char alpha[]={'A','B','C','D','E','F','G','H','I','J','K','L','M',
          'N','O','P','Q','R','S','T','U','V','W','X','Y','Z'};
int n,i,flag=1,pos;
long int tot=0;
char *permutation;
printf("\n Enter the numbr of objects (max values is 26):");
scanf("%d",&n);
permutation =(char *)malloc(n*sizeof(char));
for(i=0;i<n;i++)
    permutation[i]=alpha[i];
printf("\n The permutations are:\n");
printf("\t\t      ");
for(i=0;i<n;i++)
    printf("%c",permutation[i]);
    tot=1;
while(flag)
    {
    pos=-1;
    for(i=n-1;i>=1;i--)
        {
        if(permutation[i-1]<permutation[i])
             {
             pos=i-1;
             flag=1;
             break;
             }
        }
        if(pos==-1)
            {
            flag=0;
            break;
            }
    replace_min(permutation,n,pos);
    sort(permutation,n,pos);
   printf("\n");
    printf("\t\t      ");
    for(i=0;i<n;i++)
        printf("%c",permutation[i]);
    //tot++;
    //getche();
    }
//printf("\n Total number of permutation is: %ld",tot);
return 0;
}
void sort(char *permutation,int n,int pos)
{
    int i,j;
   char temp='A';
    for(i=pos+1;i<n-1;i++)
        {
        for(j=pos+1;j<n-1;j++)
            {
            if(permutation[j]>permutation[j+1])
                {
                temp=permutation[j+1];
                permutation[j+1]=permutation[j];
                permutation[j]=temp;
                }
            }
        }
  return;
}
void replace_min(char *permutation,int n,int pos)
{
  char min='Z',temp;
  int k,min_pos=0;
  for(k=pos+1;k<n;k++)
    {
        if(permutation[k]>permutation[pos])
            {
            if(permutation[k]<min)
                {
                min=permutation[k];
                min_pos=k;
                }
            }
    }
    temp=permutation[min_pos];
    permutation[min_pos]=permutation[pos];
    permutation[pos]=temp;
    return;
}

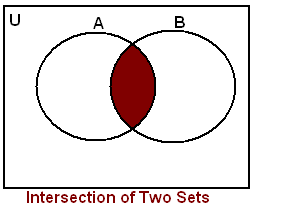
Intersection of Sets

To find intersection of two sets through C

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
void inter_set(int *s1,int*s2,int n,int m);
int main()
{
int n,m,i;
int *s1,*s2;
printf("\n Enter the number of elements in the sets:");
scanf("%d %d",&n,&m);
s1=(int *)malloc(n*sizeof(int));
s2=(int *)malloc(m*sizeof(int));
printf("\n Enter the elements of the set 1:");
for(i=0;i<n;i++)
{
printf("\n Enter the element %d:",i+1);
scanf("%d",&s1[i]);
}
printf("\n Enter the elements of the set 2:");
for(i=0;i<m;i++)
{
printf("\n Enter the element %d:",i+1);
scanf("%d",&s2[i]);
}
inter_set(s1,s2,n,m);
return 0;
}
void inter_set(int *s1,int*s2,int n,int m)
{
int *s,i=0,j,k;
int flag=0;
s=(int *)malloc((m<n ? m: n)*sizeof(int));
for(j=0;j<m;j++)
{
for(k=0;k<n;k++)
{
if(s2[j]==s1[k])
{
flag=1;
break;
}
}

if(flag==1)
{
s[i]=s2[j];
         i++;
flag=0;
}
 if(flag==0)
continue;
 }
 if(i==0)
printf("\n Intersection is Null:");
else
{
  printf("\n Intersection of the entered sets is:");
  printf("\n { ");
  for(j=0;j<i-1;j++)
printf(" %d,",s[j]);
  printf(" %d }\n ",s[i-1]);
}


return;
}

Union of Sets

This C program finds the Union of two Sets (atleast one of is non-empty)
#Task- Apply recursion to the program below to find Union of finite number of sets

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
void union_set(int *s1,int*s2,int n,int m);
int main()
{
int n,m,i;
int *s1,*s2;
printf("\n Enter the number of elements in the sets:");
scanf("%d %d",&n,&m);
s1=(int *)malloc(n*sizeof(int));
s2=(int *)malloc(m*sizeof(int));
printf("\n Enter the elements of the set 1:");
for(i=0;i<n;i++)
{
printf("\n Enter the element %d:",i+1);
scanf("%d",&s1[i]);
}
printf("\n Enter the elements of the set 2:");
for(i=0;i<m;i++)
{
printf("\n Enter the element %d:",i+1);
scanf("%d",&s2[i]);
}
union_set(s1,s2,n,m);
return 0;
}
void union_set(int *s1,int*s2,int n,int m)
{
int *s,i,j,k;
int flag=0;
s=(int *)malloc((m+n)*sizeof(int));
for(i=0;i<n;i++)
s[i]=s1[i];
for(j=0;j<m;j++)
{
for(k=0;k<n;k++)
{
if(s2[j]==s[k])
{
flag=1;
break;
}
}

if(flag==1)
{
flag=0;
continue;
         }
else
      if(flag==0)
{
s[i]=s2[j];
i++;
flag=0;
}
}
  printf("\n Union of the entered sets is:");
  printf("\n { ");
  for(j=0;j<i-1;j++)
printf(" %d,",s[j]);
  printf(" %d }\n ",s[i-1]);



}

Calculating Factorial in Python

Post by Maths.

A simple program in Python to calculate the factorial of an natural number:

#File: fact.py
#A simple program
def main():
    print "Factorial Function"
    x=input("Enter a natural number:")
    l=1
    for i in range(x):
        l=l*x
        x=x-1
    print l
main()

Run the python interpreter from the folder where the file (fact.py) is residing and import it as shown below:


administrator@ubuntu:~/python$ python
Python 2.7.4 (default, Apr 19 2013, 18:28:01)
[GCC 4.7.3] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> import fact
Factorial Function
Enter a natural number:350
123587405826548875014395199766546457224532073946919515879429330230093035357491314216934583295011178445941552109432761532449767761892237043444942213964090091669490545661255111334533069825455607852789836451585122902099649977304226794874840601811017764137584868137504975397325925882541777117706619490238363409254589994079334626893194608016888986949684994333459029365214555784862353939102567266745712846824819004146064184543888123533464975621179287075018586481357643313075153359002713294611632614208134036650116689052585573350955360246170451786972351365370405722036294385680478287278827977511411909071460914807681131728232182991517416470483157998067487290163200000000000000000000000000000000000000000000000000000000000000000000000000000000000000
>>>

Modified Euler's Method for Numerical Solution of first order Differential Equation

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<math.h>
double dfxy(double x,double y);
FILE *fp;
int main(int argc, char* argv[])
{
double x0,y0,h,x,*xi,*yi,temp=0.0;
char c;
int n,i;
if(argc==1)
    {
    printf("\n Enter the value of h (interval-width):");
    scanf("%lf",&h);
    printf("\n Enter the initial value of x:");
    scanf("%lf",&x0);
    printf("\n Enter the initial value of y:");
    scanf("%lf",&y0);
    printf("\n Enter the value of x at which y is calculated:");
    scanf("%lf",&x);
    xi=(double *)malloc((n+1)*sizeof(double));
    yi=(double *)malloc((n+1)*sizeof(double));
    }
else if(argc==2)
    {
    /*fp=fopen(argv[1],"r");
    fscanf(fp,"%d",&n);
    fscanf(fp,"%lf",&lower_limit);
    fscanf(fp,"%lf",&upper_limit);
    xi=(double *)malloc((n+1)*sizeof(double));
    yi=(double *)malloc((n+1)*sizeof(double));*/
    }
else
    {
    printf("\n Invalid arguments, program will terminate:");
    exit(1);
    }
n=(x-x0)/h;
xi[0]=x0;
yi[0]=y0;
printf("\n\tX\t\t\tY\n");
printf("\tf(%+lf)\t\t=%+lf",xi[0],yi[0]);
i=1;
while(x0!=x)
    {
    yi[i]=yi[i-1]+dfxy(xi[i-1],yi[i-1])*h;
    x0=x0+h;
    xi[i]=x0;
    //printf("\n >>>>>>>>%lf",yi[i]);
    do
    {
    temp=yi[i];
    yi[i]=yi[i-1]+(h/2)*(dfxy(xi[i-1],yi[i-1])+dfxy(xi[i],yi[i]));
    //printf("\n >>>>>>>>%lf",yi[i]);
    }while(fabs(temp-yi[i])>0.00001);
    i++;
    xi[i]=x0;
    yi[i]=temp;
    printf("\n\tf(%+lf)\t\t=%+lf",xi[i],yi[i]);
    }
printf("\n");
return 0;
}
double dfxy(double x,double y)
    {
    return (x*x+y);
    }

Euler's Method for Numerical Solution of first order Differential Equation

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<math.h>
double dfxy(double x,double y);
FILE *fp;
int main(int argc, char* argv[])
{
double x0,y0,h,x,*xi,*yi,temp=0.0;
int n,i;
if(argc==1)
    {
    printf("\n Enter the value of h (interval-width):");
    scanf("%lf",&h);
    printf("\n Enter the initial value of x:");
    scanf("%lf",&x0);
    printf("\n Enter the initial value of y:");
    scanf("%lf",&y0);
    printf("\n Enter the value of x at which y is calculated:");
    scanf("%lf",&x);
    xi=(double *)malloc((n+1)*sizeof(double));
    yi=(double *)malloc((n+1)*sizeof(double));
    }
else if(argc==2)
    {
    /*fp=fopen(argv[1],"r");
    fscanf(fp,"%d",&n);
    fscanf(fp,"%lf",&lower_limit);
    fscanf(fp,"%lf",&upper_limit);
    xi=(double *)malloc((n+1)*sizeof(double));
    yi=(double *)malloc((n+1)*sizeof(double));*/
    }
else
    {
    printf("\n Invalid arguments, program will terminate:");
    exit(1);
    }
n=(x-x0)/h;
xi[0]=x0;
yi[0]=y0;
printf("\n\tX\t\t\tY\n");
printf("\t%+lf\t\t%+lf",xi[0],yi[0]);
i=1;
while(x0!=x)
    {
    yi[i]=yi[i-1]+dfxy(xi[i-1],yi[i-1])*h;
    x0=x0+h;
    xi[i]=x0;
    printf("\n\t%+lf\t\t%+lf",xi[i],yi[i]);
    }
printf("\n");
//printf("\n Value of the integral using Trapezoidal Rule is %+.8lf\n",invert==0 ? (h/2.0)*temp:-(h/2.0)*temp);
return 0;
}
double dfxy(double x,double y)
    {
    return (x+y);
    }